Sphere - Cone Intersection
4 minute read.
During my bachelor’s thesis about view culling for VR using cones as view volumes, I meditated on different intersection algorithms. Find my last blog post on this topic here: Axis-Aligned Bounding Box - Cone Intersection.
As celebration that the blog post got accepted into the table of static object intersection algorithms on realtimerendering.com, here is my slightly enhanced version of David Eberly’s method I found for cone-sphere intersection.

The overall idea is to check whether the distance of the sphere’s center to the cone’s surface is closer less than its radius. Find this situation outlined in the following figure:
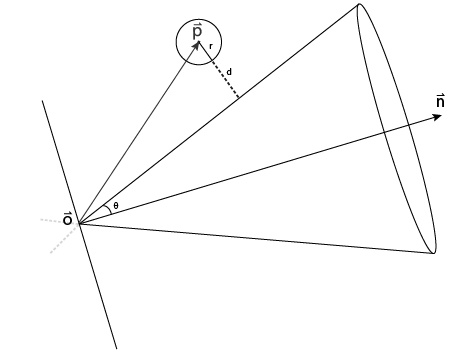
Computing the distance of the center to the cone is rather cumbersome and we want our solution to be as performant as possible, so instead we expand the cone by the radius in every direction to then be able to do a simple point-cone test.
This can be easily achieved by offsetting the origin back along its normal, as shown by the arrow in the opposite direction of the normal:
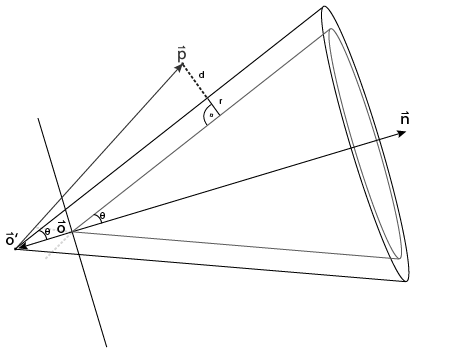
To expand the cone’s surface by r, we move back the cone’s origin by -r/sin(theta) (theta being the
cone’s angle) along the normal. You will quickly realize that in most cases the new origin is now further
away from the original origin than the radius r and this results in false positives if the sphere is around
the apex of the cone.
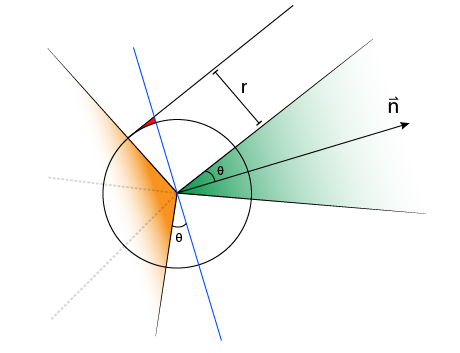
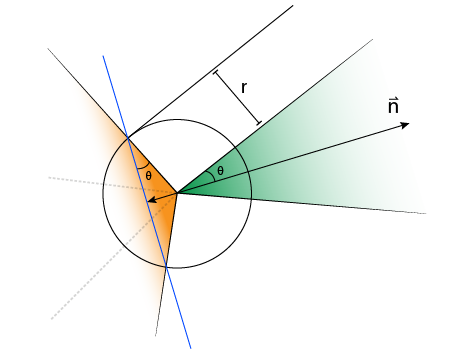
We therefore split our test into two cases: the case half-space where testing against our offset cone is valid and the half-space in which we instead test the cone’s origin with the sphere. The difference with Eberly’s method is the realization that two cases suffice, where Eberly differentiates “behind the offset cone”, “in front using the offset cone” and “in front using the sphere”.
By realizing we can instead split into two cases we save a plane test, but trade that off for always having
to compute sin(theta), even if the sphere is on the half-space behind the offset cone.
But, this sine can be precomputed once for the cone, which works especially well for view culling where
the field of view generally stays the same.
How to offset the original cone’s half-space is shown in the following sketch:
Resources and Implementation
For a more thorough explanation including the formulas for offset of plane and origin, please refer to my bachelor’s thesis (p. 14).
Find my implementation of this method in the code of the open-source magnum graphics engine and its documentation here, as well as extensive tests and a benchmark.