Jul 05 2018 Axis-Aligned Bounding Box - Cone Intersection

~ 4 Minute Read.

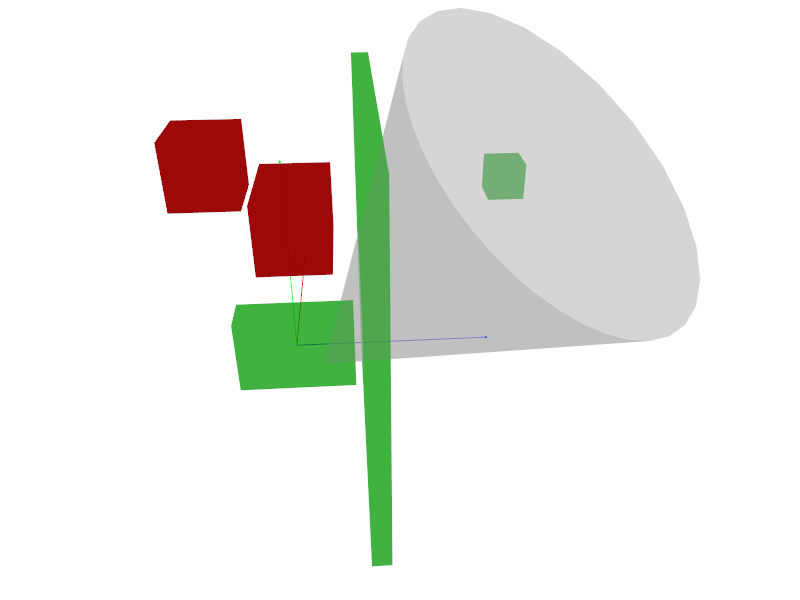
During my bachelor’s thesis about view culling using cone view volumes, I had to figure out whether an axis-aligned bounding box overlaps a cone.

Visualization of aabb cone intersection.

And when I say figure out, I mean that I didn’t find any resources online (even the comprehensive table on realtimerendering.com had an empty cell here). Whether this is because I don’t know how to use google search, nobody had use for this before (e.g. physics engines require more than just whether two objects intersect) or because it’s so simple that nobody wrote it down (which would mean I wasted many many hours over this not seeing the easy way)… here is the solution I came up with.

Important: I describe a method here that determines whether an AABB intersects with a cone, not trying to calculate the full intersection volume.

Disclaimer: Algorithm is not valid!

I want to thank Eric Haines and David Eberly for their efforts to thoroughly inspecting this algorithm, leading to the following input for which it outputs a false positive:

Cone origin = {0, 0, 0}
Cone direction = normalize({1, 0.5, -1})

Cone angle = 2*0.464
Box min point = {0, 2, -1}
Box max point = {4, 4, 1}
Box center = 0.5*(min + max)
Box extents = 0.5*(max – min)

Sadly, I am currently not able to make the time to look for a solution/fix. In case you find a solution, please drop an email: squareys@googlemail.com

Algorithm

The axis-aligned constraint is pretty great here: you can simplify the 3D problem into a 2D problem by omitting one axis at a time. So that is what we’re going to do; for each axis only look at the other two.

Say the axis we chose is x for more practical explanation. Next we would extend the faces whose normals are parallel to x to infinite planes. This allows us to ray-cast the cone axis through these planes and figure out where they intersect. Since our normal is {1.0f, 0.0f, 0.0f} for this plane, the line-plane intersection formula can be simplified quite a bit even.

As the image shows, we have now reduced the problem in 3D (left) to a problem in 2D (right). We have a last problem, though: the intersection of the cone surface usually does not result in a perfect circle but an ellipse.

Instead of trying to intersect that oval/elliptic area with the square, we can instead find the point that is closest to the cone axis—this point is also closest to the cone. If it is inside the cone, we found a point that is shared by both objects and know that they intersect. This is therefore now a point cone test.

If it does not intersect, we still need to check all the other faces! If none of those result in intersection, the objects do not intersect.

Code

If you’re interested in an implementation, please have a look at the one I contributed to the Magnum Engine: find the code here and the documentation here. You will also find extensive tests there, which you can use as a starting point for trying to break this method.

May I have saved you some time :)

Written in 45 minutes, edited in 15 minutes.

Al­go­rithm

Code

Algorithm